
Las colas se forman por la diferencia de tiempo que aparece entre la llegada de un encargo y la emisión del servicio para satisfacerlo. Cuanto mayor es la capacidad de servicio descrita, menor es la probabilidad de formación de colas.
La mejor gestión de colas es la que sale más rentable, económicamente hablando, para la empresa. Es decir, no se trata de gestionar para llegar a no tener colas, sino de tenerlas en consideración a la hora de establecer las soluciones más adecuadas para la economía de la empresa. Dicho de manera popular, debe buscarse el equilibrio entre los tiempos de espera (colas) y el balance económico de las operaciones.
Los cuatro parámetros que definen un problema de colas son:
- El patrón de las tasas de llegada. Puede ser aleatoria –definida o indefinida- (caso en el que trabajamos con funciones estadísticas de probabilidad) o conocida. Por ejemplo: una máquina se para y está esperando atención → se pueden tener los datos concretos (conocida) o atender a la probabilidad de que eso ocurra (aleatoria).
- El patrón de la tasa de servicio. De la misma manera puede ser conocido o aleatorio.
- El número de unidades de servicio. Determinado por problemas del tipo ¿cuántos trabajadores son necesarios para la operación de un determinado número de máquinas? Se diferencia entre un solo servicio y las operaciones multiservicios.
- El patrón de la selección de servicio. Alude a las prioridades de atención de pedidos. No siempre se recurre a la táctica evidente de atender primero al que primero llegó. Hay multitud de razones para programar la operación con una alternativa.
Una vez identificado el problema de colas, se debe pensar en la solución. La ortodoxia en el sector indica que las resoluciones a los problemas de colas se distinguen en dos grandes grupos:
- Analíticos
- De simulación
Soluciones analíticas
En este tipo de soluciones mandan los modelos estadísticos. Uno de los más empleados para la estimación del patrón de llegadas es el modelo de Poisson, que se corresponde con la expresión:

El ábaco anexo recoge el comportamiento del planteamiento estadístico definido por Poisson.
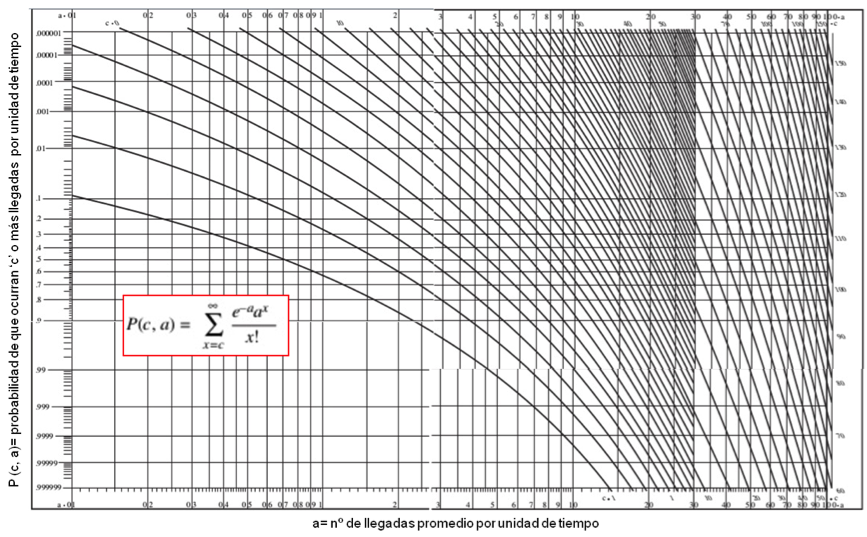
Si se admite la citada distribución de Poisson, implícitamente se conviene que el tiempo entre llegadas sigue una distribución exponencial con el mismo parámetro ‘a’. Según:
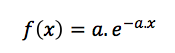
Se trata de una distribución conocida que tiene las siguientes cualidades probabilísticas:

En este caso la media se puede interpretar como el tiempo medio entre pedidos (llegadas).
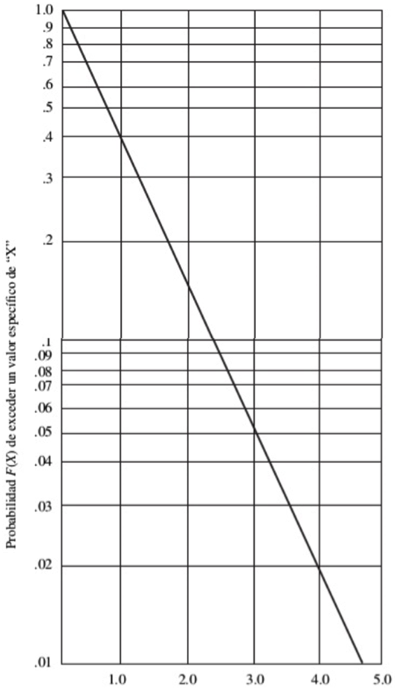
La distribución exponencial sigue un comportamiento como el que se muestra en la gráfica adjunta. Esta función responde a la probabilidad de exceder un valor específico de la variable ‘x’.
Las categorías de la teoría de colas que se encuentran dentro del campo de aplicación del modelo de Poisson son:
- Un solo servidor y cualquier distribución de tiempos de servicio
- Un solo servidor y tiempo de servicio exponencial
- Un solo servidor y tiempo de servicio constante
- Número finito de servidores y tiempo de servicio exponencial
- Número finito de servidores y tiempo de servicio constante
Para cada uno de estos grupos se han diseñado ecuaciones específicas devolviendo las realidades cuantitativas sobre:
- El tiempo medio de demora de la línea de espera
- El promedio de pedidos (llegadas o encargos) que llegan a la línea de espera
Antonio D. Cansinos Bajo
